Zen 3.1

comments/feedback

Updated post: Go vs Java: Decoding Billions of Integers Per Second

tl;dr

• Source code
• Let me start by saying that I am not that happy with the performance numbers I got. It probably has more to do with my familiarity and expertise with Go than anything else. But still…
• Having said that, I am pleasantly surprised how much faster some of the integer compression algorithms are compare to standard compression algorithms such as gzip, LZW and even snappy.
• There’s no one size fits all solution. There’s always tradeoffs between compression ratio and compression/decompression speed. So depending on the type of integer data and how fast you want to encode/decode, you will need to choose the right solution.
• Gzip does probably the best job in compression ratio but worst in terms of encoding/decoding performance.
• Delta BP32 (IntegratedBinaryPacking in JavaFastPFOR) performs the best (ratio, encoding/decoding speed) for sorted integer arrays such as timestamps.
• I would love it if someone can run these tests on a faster machine and send me the results. I would be happy to put them into the spreadsheet.

Go Learn Project #6 - Integer Compression

It’s been 4 weeks since my last post and I have been BUSY! My day job has been busier than ever (in a good way) and has taken over many of my nights and weekends. However, I’ve not forgotten the “Go Learn” project and continued to tinker with Go as I find time.

For “Go Learn” project #6, I decided to port JavaFastPFOR over to Go. The JavaFastPFOR repo actually is a collection of integer encoding/decoding algorithms. However, the more interesting ones are the ones created by Daniel Lemire, including FastPFOR, BP32, BP128, etc. To borrow from the repo’s readme:

[JavaFastPFOR] is a library to compress and uncompress arrays of integers very fast. The assumption is that most (but not all) values in your array use less than 32 bits. These sort of arrays often come up when using differential coding in databases and information retrieval (e.g., in inverted indexes or column stores).

Some CODECs (“integrated codecs”) assume that the integers are in sorted orders. Most others do not.

Thank You, Daniel Lemire

As you may have noticed, this is the second Daniel Lemire project that I’ve ported over. The previous one is Bitmap Compression using EWAH in Go.

Danile Lemire is a computer science professor at TELUQ (Université du Québec) where he teaches primarily online. He specializes in Databases, Data Warehousing and OLAP, Recommender Systems and Collaborative Filtering, and Information Retrieval.

I won’t elaborate on how knowledgeable he is here because you can easily tell by reading his papers and blogs. I do want to mention how Daniel has been extremely helpful on my porting effort. He’s provided tremendous guidance and support, and went even as far as providing me access to one of his machines for running performance tests.

So thank you Daniel!

Decoding Billions of Integers per Second Through Vectorization

This project is inspired by Danile’s blog post, Fast integer compression: decoding billions of integers per second, and paper. As the paper states:

In many important applications—such as search engines and relational database systems—data is stored in the form of arrays of integers. Encoding and, most importantly, decoding of these arrays consumes considerable CPU time. Therefore, substantial effort has been made to reduce costs associated with compression and decompression

As part of this research, Daniel also made his code available in C++ and Java. The Go port is based on JavaFastPFOR.

However, because Go has no access to the SSE instruction sets (well, not without getting into C or assembly), I was not able to port over the SIMD versions of the algorithms.

The Port

The Go port is available on github. In this version, I’ve proted over six algorithms, including

• FastPFOR
• BP32 (BinaryPacking in JavaFastPFOR)
• Delta BP32 (IntegratedBinaryPacking in JavaFastPFOR)
• ZigZag BP32 (BP32 with Delta encoding using ZigZag encoding method.)
• VariableBytes
• Delta VariableBytes (Integrated VariableBytes in JavaFastPFOR)

I won’t go into details of how each of these algorithms work. If you are interested, I strongly encourage you to go read Daniel’s paper.

The Benchmarks

To benchmark these algorithms, I’ve created 5 sets of data.

• Clustered - This is a generated list of random and sorted integers based on the clustered model.
• Uniform - This will generate a “uniform” list of sorted integers.
• Timestamps - This is a list of timestamps in sorted order, extracted from another data set that’s mainly network monitoring data. The timestamps are epoch time (seconds since 1970). It has long runs of the same timestamp because the dataset contains many entries per second.
• IP Addresses - This is a data set that contains a 32-bit integer representation of IPv4 addresses. This data set is NOT sorted.
  • In the real-world, one probably wouldn’t compress IP addresses like that. One would probably use dictionary encoding for the IPs, then encode the dictionary keys.
  • The dictionary keys will likely be much smaller numbers, which means it will compress fairly well.
• Latencies - This list of integers represent latencies on the network. It is also unsorted.

Timestamps, IP addresses, and Latencies are essentially 3 columns from another dataset.

Along with benchmarking the integer encoding algorithms, I also benchmarked the Go implementations of Gzip, LZW and Snappy. Both Gzip and LZW are part of the Go standard library. Snappy is a separate project implemented by the Go developers.

The Results

All benchmarks are performed on a machine with Intel® Xeon® CPU E5-2609 0 @ 2.40GHz.

Compression Ratio (Lower is Better)

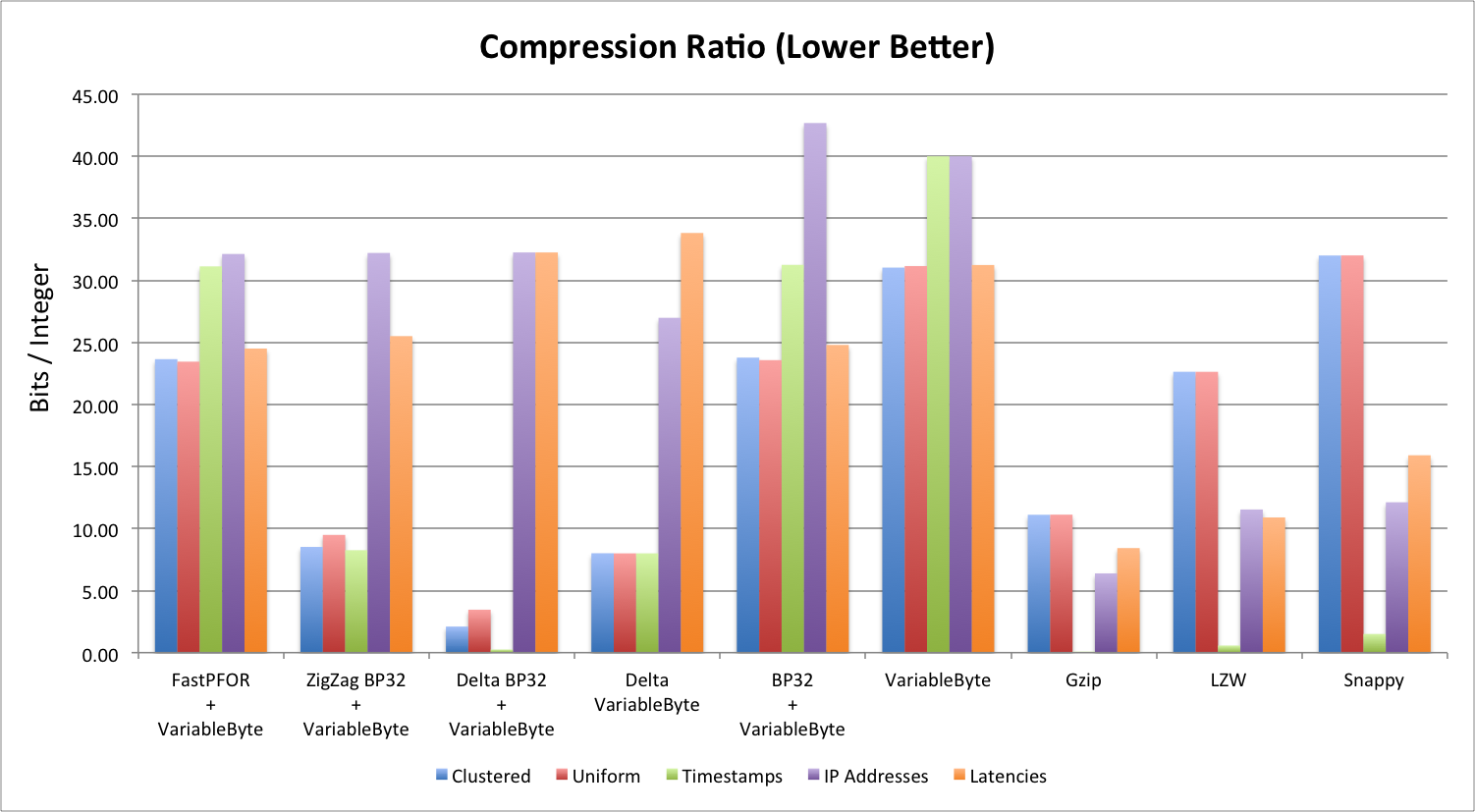
Compression ratio is measured in bits/integer. Before compression, the integers we are compressing are all 32-bit integers. This chart shows us how many bits are used for each integer after compression.

There are a few things you can observe from this chart:

• Sorted integer lists ALWAYS perform better (ratio and speed) than unsorted integer lists.
• Sometimes the compressed size is LARGER than the uncompressed size. This is because some of these algorithms use extra space to store encoding meta information.
• Gzip, in general, has the best compression ratio.
• Delta BP32 performs the best for sorted lists, but really has problems with unsorted lists.

Compression Speed (Higher is Better)

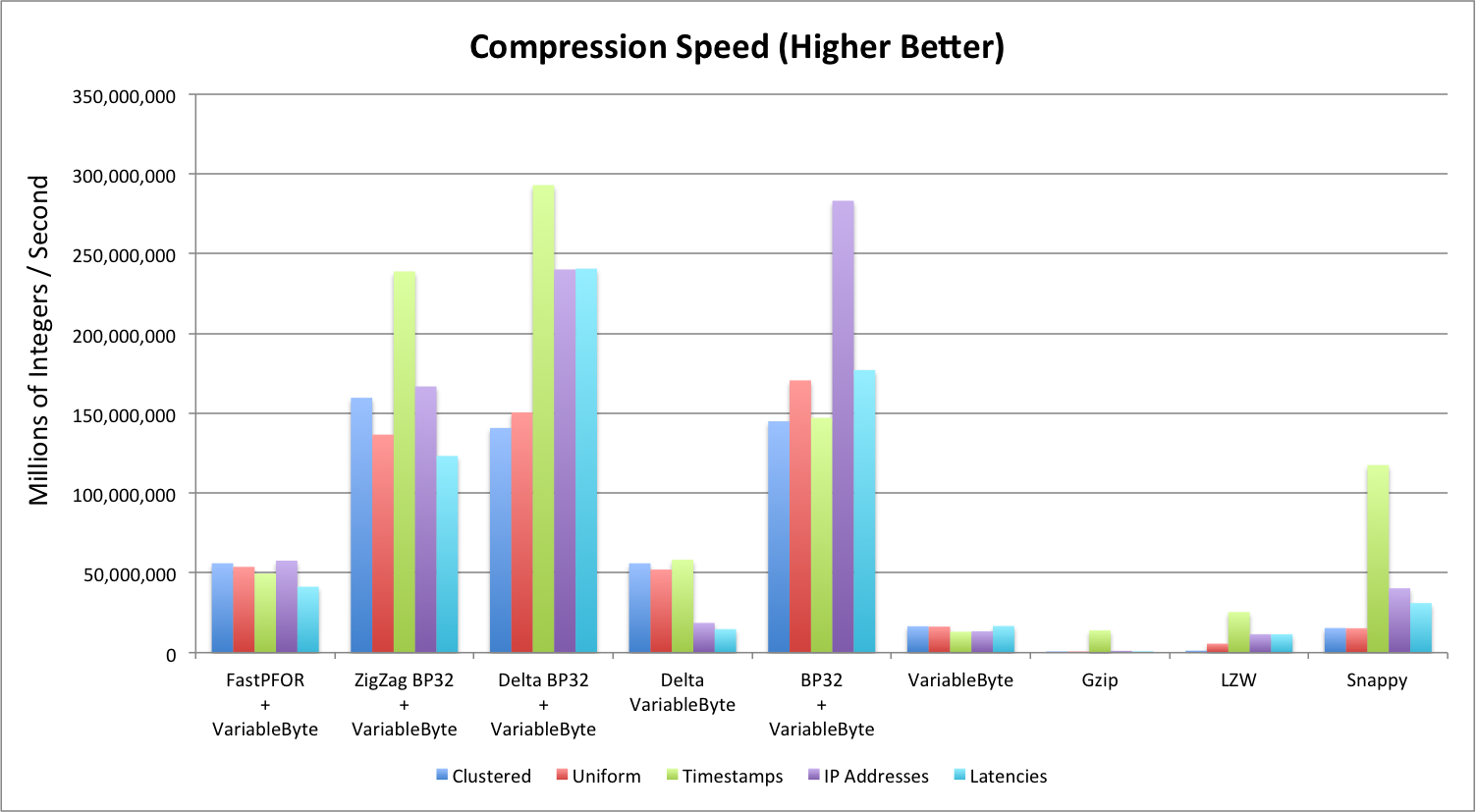
Compression speed is measured in millions of integers per second (MiS). Note that:

• Delta BP32 by far has the best compression speed across different data sets.
• BP32 does a fairly decent job compressing as well, but its compression ratio is fairly poor.
• Gzip and LZW perfom the most poorly.

Decompression Speed

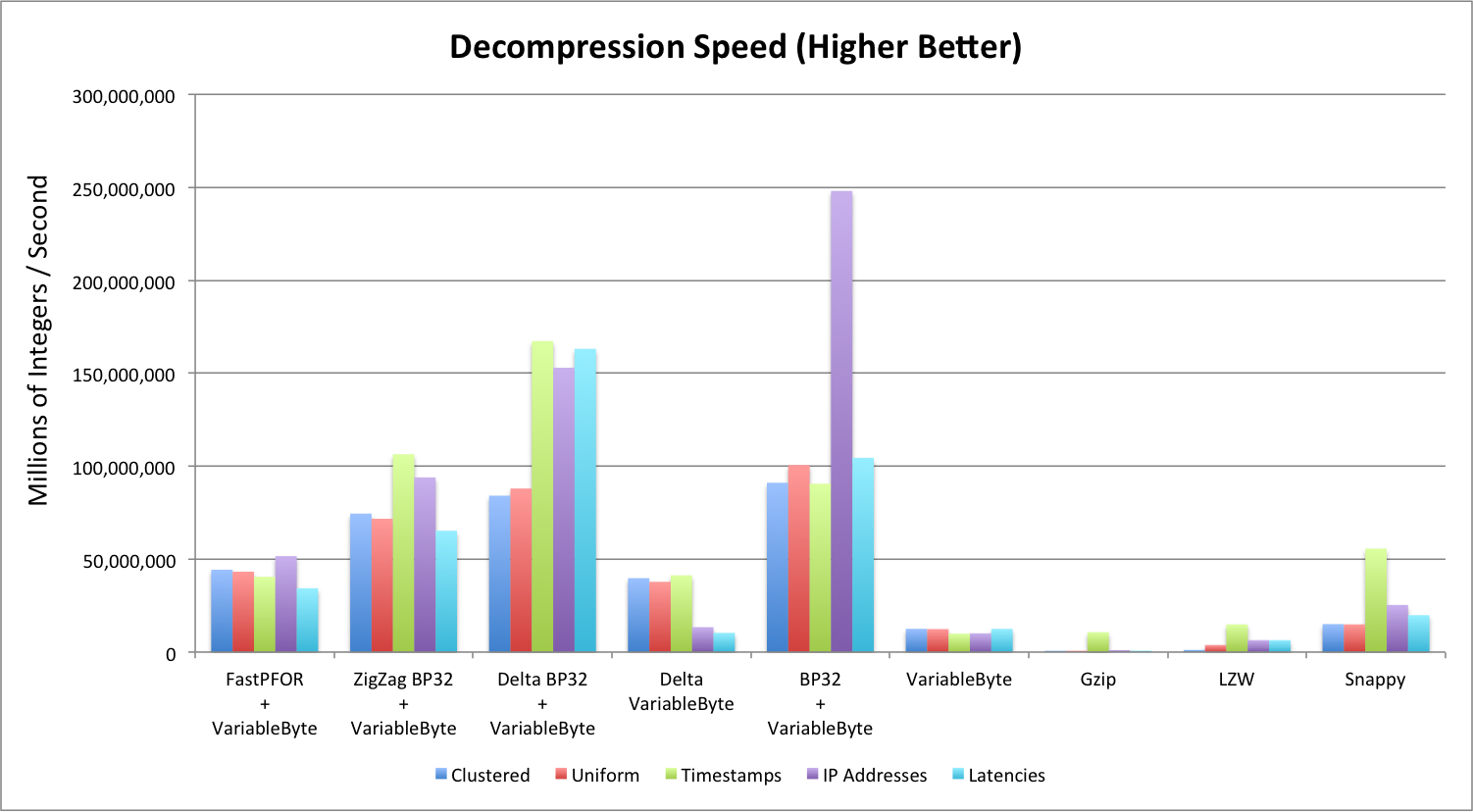
Decompression speed is measured in millions of integers per second (MiS). Note that:

• Again, Delta BP32 does the best across different data sets, and gzip/LZW did the poorest.
• BP32 decoded extremely fast for sorted timestamps that have large runs of the same timestamps.
• FastPFOR seems to perform the most consistently for integer compression algorithms. (For compression as well.)

The Conclusions

• For encoding sorted numbers, Delta BP32 has the best combination of compression ratio, and encoding/decoding speed.
• For encoding unsorted numbers, Snappy seems like a good alternative.
• For long term storage, it might be worth considering gzip. It provides the best compression ratio for data that may not be accessed for a long while.

The Raw Result

The following is a Google spreadsheet that contains the raw result set.

comments/feedback